Constructing Predictive Fashions: Logistic Regression in Python

Picture by Writer

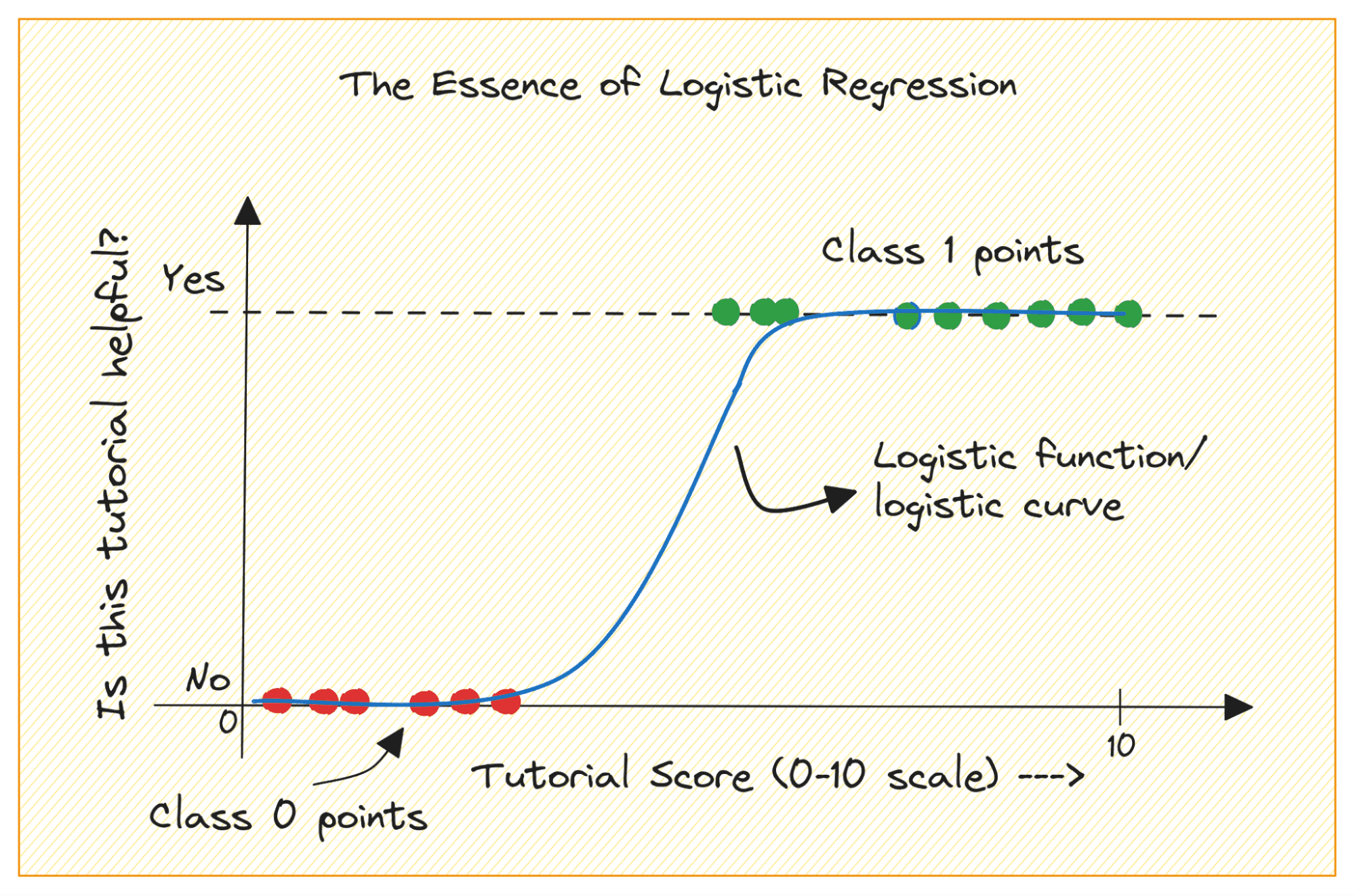
If you find yourself getting began with machine studying, logistic regression is likely one of the first algorithms you’ll add to your toolbox. It is a easy and sturdy algorithm, generally used for binary classification duties.

Contemplate a binary classification downside with lessons 0 and 1. Logistic regression matches a logistic or sigmoid perform to the enter knowledge and predicts the chance of a question knowledge level belonging to class 1. Fascinating, sure?

On this tutorial, we’ll study logistic regression from the bottom up protecting:

• The logistic (or sigmoid) perform
• How we transfer from linear to logistic regression
• How logistic regression works

Lastly, we’ll construct a easy logistic regression mannequin to classify RADAR returns from the ionosphere.

 
Earlier than we be taught extra about logistic regression, let’s evaluate how the logistic perform works. The logistic (or sigmoid perform) is given by:

If you plot the sigmoid perform, it’ll appear like so:

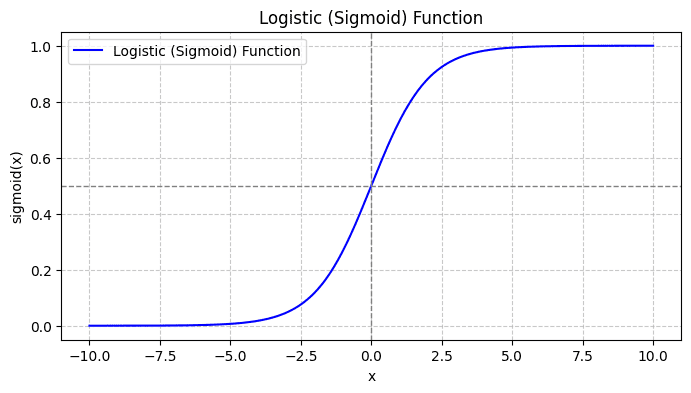
From the plot, we see that:

• When x = 0, σ(x) takes a worth of 0.5.
• When x approaches +∞, σ(x) approaches 1.
• When x approaches -∞, σ(x) approaches 0.

So for all actual inputs, the sigmoid perform squishes them to tackle values within the vary [0, 1].

 
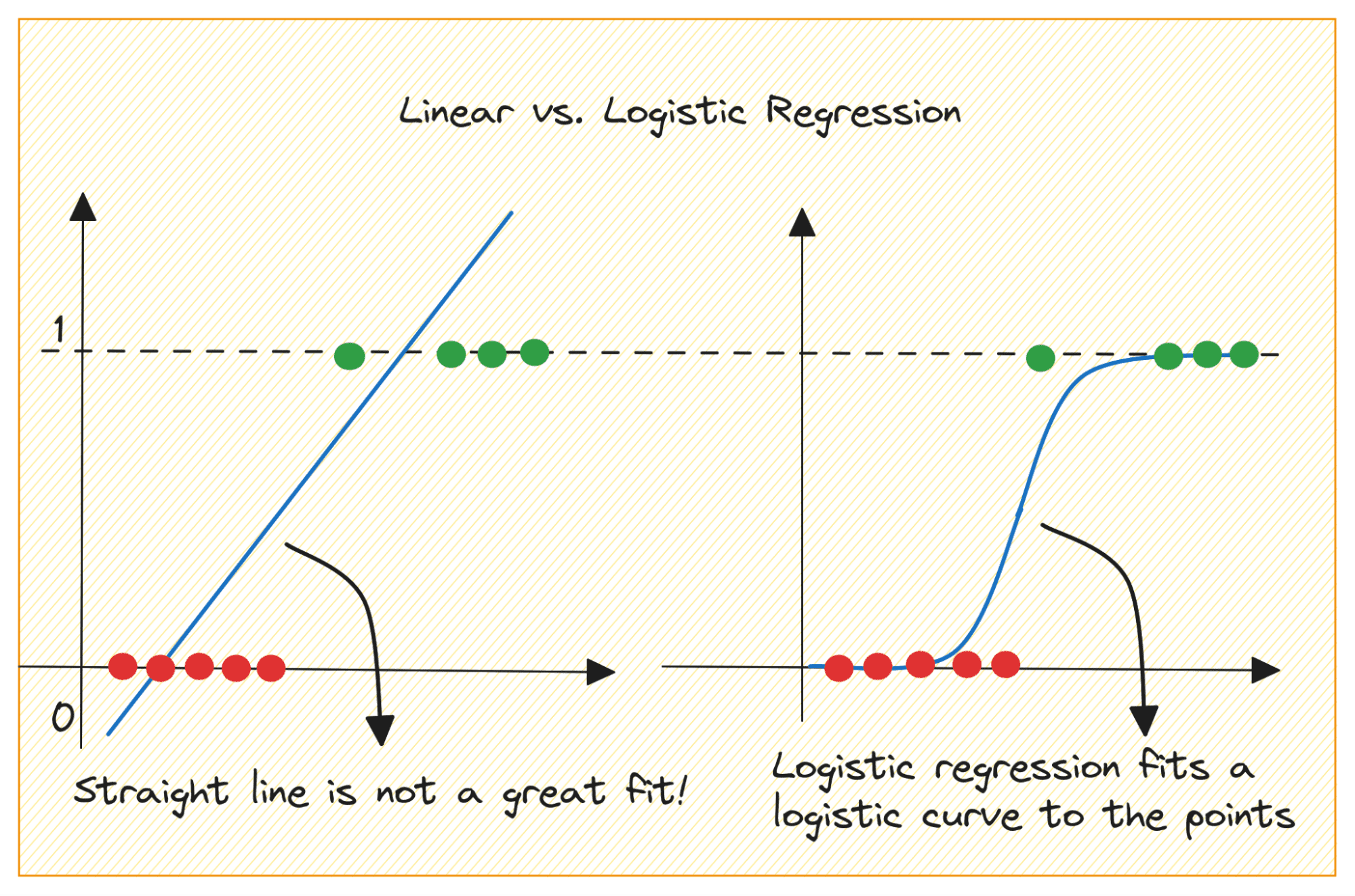
Let’s first talk about why we can not use linear regression for a binary classification downside.

In a binary classification downside, the output is categorical label (0 or 1). As a result of linear regression predicts continuous-valued outputs which might be lower than 0 or larger than 1, it doesn’t make sense for the issue at hand.

Additionally, a straight line might not be the perfect match when the output labels belong to one of many two classes.

Picture by Writer

So how will we go from linear to logistic regression? In linear regression the anticipated output is given by:

The place the βs are the coefficients and X_is are the predictors (or options).

With out lack of generality, let’s assume X_0 = 1:

So we will have a extra concise expression:

In logistic regression, we want the anticipated chance p_i within the [0,1] interval. We all know that the logistic perform squishes inputs in order that they tackle values within the [0,1] interval.

So plugging on this expression into the logistic perform, now we have the anticipated chance as:

 
So how do we discover the perfect match logistic curve for the given knowledge set? To reply this, let’s perceive most probability estimation.

Most Probability Estimation (MLE) is used to estimate the parameters of the logistic regression mannequin by maximizing the probability perform. Let’s break down the method of MLE in logistic regression and the way the associated fee perform is formulated for optimization utilizing gradient descent.

Breaking Down Most Probability Estimation

 
As mentioned, we mannequin the chance {that a} binary consequence happens as a perform of a number of predictor variables (or options):

Right here, the βs  are the mannequin parameters or coefficients. X_1, X_2,…, X_n are the predictor variables.

MLE goals to seek out the values of β that maximize the probability of the noticed knowledge. The probability perform, denoted as L(β), represents the chance of observing the given outcomes for the given predictor values below the logistic regression mannequin.

Formulating the Log-Probability Operate

 
To simplify the optimization course of, it is common to work with the log-likelihood perform. As a result of it transforms merchandise of possibilities into sums of log possibilities.

The log-likelihood perform for logistic regression is given by:

 
Now that we all know the essence of log-likelihood, let’s proceed to formulate the associated fee perform for logistic regression and subsequently gradient descent for locating the perfect mannequin parameters

Price Operate for Logistic Regression

 
To optimize the logistic regression mannequin, we have to maximize the log-likelihood. So we will use the detrimental log-likelihood as the associated fee perform to reduce throughout coaching. The detrimental log-likelihood, also known as the logistic loss, is outlined as:

The objective of the training algorithm, subsequently, is to seek out the values of ? that reduce this value perform. Gradient descent is a generally used optimization algorithm for locating the minimal of this value perform.

Gradient Descent in Logistic Regression

Gradient descent is an iterative optimization algorithm that updates the mannequin parameters β in the wrong way of the gradient of the associated fee perform with respect to β. The replace rule at step t+1 for logistic regression utilizing gradient descent is as follows:

The place α is the training charge.

The partial derivatives might be computed utilizing the chain rule. Gradient descent iteratively updates the parameters—till convergence—aiming to reduce the logistic loss. Because it converges, it finds the optimum values of β that maximize the probability of the noticed knowledge.

Now that you understand how logistic regression works, let’s construct a predictive mannequin utilizing the scikit-learn library.

We’ll use the ionosphere dataset from the UCI machine studying repository for this tutorial. The dataset includes 34 numerical options. The output is binary, considered one of ‘good’ or ‘dangerous’ (denoted by ‘g’ or ‘b’). The output label ‘good’ refers to RADAR returns which have detected some construction within the ionosphere.

Step 1 – Loading the Dataset

 
First, obtain the dataset and browse it right into a pandas dataframe:

import pandas as pd
import urllib

url = "https://archive.ics.uci.edu/ml/machine-learning-databases/ionosphere/iphere.knowledge"
knowledge = urllib.request.urlopen(url)
df = pd.read_csv(knowledge, header=None)

Step 2 – Exploring the Dataset

Let’s check out the primary few rows of the dataframe:

# Show the primary few rows of the DataFrame
df.head()

Truncated Output of df.head()

Let’s get some details about the dataset: the variety of non-null values and the info forms of every of the columns:

# Get details about the dataset
print(df.information())

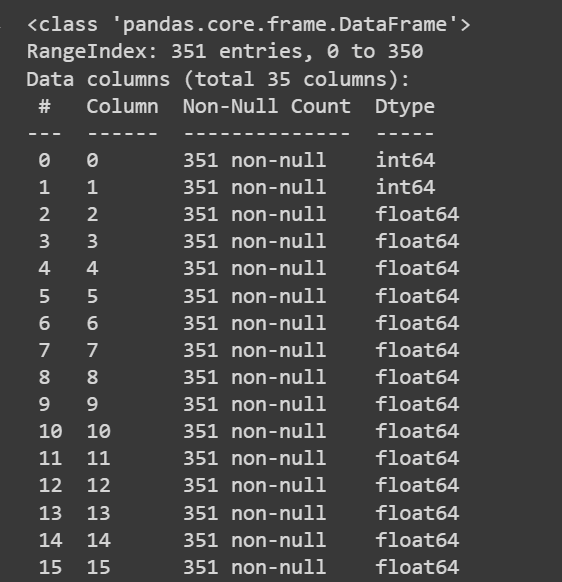Truncated Output of df.information()

As a result of now we have all numeric options, we will additionally get some descriptive statistics utilizing the describe() methodology on the dataframe:

# Get descriptive statistics of the dataset
print(df.describe())

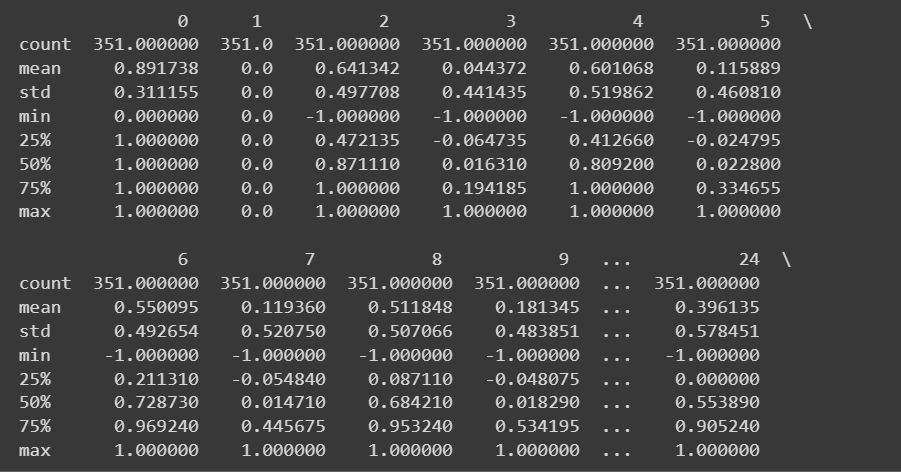
Truncated Output of df.describe()

column_names = [
"attribute_1", "attribute_2", "attribute_3", "attribute_4", "attribute_5",
"attribute_6", "attribute_7", "attribute_8", "attribute_9", "attribute_10",
"attribute_11", "attribute_12", "attribute_13", "attribute_14", "attribute_15",
"attribute_16", "attribute_17", "attribute_18", "attribute_19", "attribute_20",
"attribute_21", "attribute_22", "attribute_23", "attribute_24", "attribute_25",
"attribute_26", "attribute_27", "attribute_28", "attribute_29", "attribute_30",
"attribute_31", "attribute_32", "attribute_33", "attribute_34", "class_label"
]
df.columns = column_names

Word: This step is solely optionally available. You may proceed with the default column names should you want.

# Show the primary few rows of the DataFrame
df.head()

Truncated Output of df.head() [After Renaming Columns]

Step 3 – Renaming Class Labels and Visualizing Class Distribution

 
As a result of the output class labels are ‘g’ and ‘b’, we have to map them to 1 and 0 , respectively. You are able to do it utilizing map() or substitute():

# Convert the class labels from 'g' and 'b' to 1 and 0, respectively
df["class_label"] = df["class_label"].substitute({'g': 1, 'b': 0})

Let’s additionally visualize the distribution of the category labels:

import matplotlib.pyplot as plt

# Rely the variety of knowledge factors in every class
class_counts = df['class_label'].value_counts()

# Create a bar plot to visualise the category distribution
plt.bar(class_counts.index, class_counts.values)
plt.xlabel('Class Label')
plt.ylabel('Rely')
plt.xticks(class_counts.index)
plt.title('Class Distribution')
plt.present()

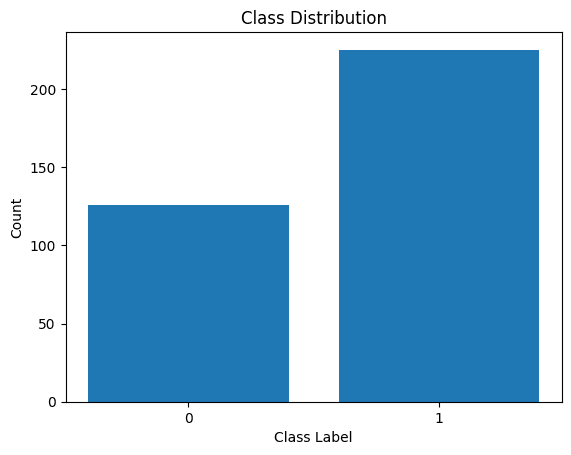
Distribution of Class Labels

We see that there’s an imbalance within the distribution. There are extra information belonging to class 1 than to class 0. We’ll deal with this class imbalance when constructing the logistic regression mannequin.

Step 5 – Preprocessing the Dataset

 
Let’s accumulate the options and output labels like so:

X = df.drop('class_label', axis=1)  # Enter options
y = df['class_label']               # Goal variable

After splitting the dataset into the practice and check units, we have to preprocess the dataset.

When there are lots of numeric options—every on a doubtlessly totally different scale—we have to preprocess the numeric options. A standard methodology is to rework them such that they observe a distribution with zero imply and unit variance.

The StandardScaler from scikit-learn’s preprocessing module helps us obtain this.

from sklearn.preprocessing import StandardScaler
from sklearn.model_selection import train_test_split

# Cut up the dataset into coaching and testing units
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

# Get the indices of the numerical options
numerical_feature_indices = checklist(vary(34))  # Assuming the numerical options are in columns 0 to 33

# Initialize the StandardScaler
scaler = StandardScaler()

# Normalize the numerical options within the coaching set
X_train.iloc[:, numerical_feature_indices] = scaler.fit_transform(X_train.iloc[:, numerical_feature_indices])

# Normalize the numerical options within the check set utilizing the skilled scaler from the coaching set
X_test.iloc[:, numerical_feature_indices] = scaler.remodel(X_test.iloc[:, numerical_feature_indices])

Step 6 – Constructing a Logistic Regression Mannequin

 
Now we will instantiate a logistic regression classifier. The LogisticRegression class is a part of scikit-learn’s linear_model module.

Discover that now we have set the class_weight parameter to ‘balanced’. It will assist us account for the category imbalance. By assigning weights to every class—inversely proportional to the variety of information within the lessons.

After instantiating the category, we will match the mannequin to the coaching dataset:

from sklearn.linear_model import LogisticRegression

mannequin = LogisticRegression(class_weight="balanced")
mannequin.match(X_train, y_train)

Step 7 – Evaluating the Logistic Regression Mannequin

 
You may name the predict() methodology to get the mannequin’s predictions.

Along with the accuracy rating, we will additionally get a classification report with metrics like precision, recall, and F1-score.

from sklearn.metrics import accuracy_score, classification_report

y_pred = mannequin.predict(X_test)
accuracy = accuracy_score(y_test, y_pred)
print(f"Accuracy: {accuracy:.2f}")

classification_rep = classification_report(y_test, y_pred)
print("Classification Report:n", classification_rep)

Congratulations, you could have coded your first logistic regression mannequin!

 
On this tutorial, we discovered about logistic regression intimately: from concept and math to coding a logistic regression classifier.

As a subsequent step, attempt constructing a logistic regression mannequin for an acceptable dataset of your alternative.

 
The Ionosphere dataset is licensed below a Inventive Commons Attribution 4.0 Worldwide (CC BY 4.0) license:

Sigillito,V., Wing,S., Hutton,L., and Baker,Okay.. (1989). Ionosphere. UCI Machine Studying Repository. https://doi.org/10.24432/C5W01B.

Bala Priya C is a developer and technical author from India. She likes working on the intersection of math, programming, knowledge science, and content material creation. Her areas of curiosity and experience embody DevOps, knowledge science, and pure language processing. She enjoys studying, writing, coding, and occasional! At present, she’s engaged on studying and sharing her information with the developer group by authoring tutorials, how-to guides, opinion items, and extra.