Unveiling Hidden Patterns: An Introduction to Hierarchical Clustering

If you’re familiarizing your self with the unsupervised studying paradigm, you will find out about clustering algorithms. 

The purpose of clustering is commonly to grasp patterns within the given unlabeled dataset. Or it may be to discover teams within the dataset—and label them—in order that we will carry out supervised studying on the now-labeled dataset. This text will cowl the fundamentals of hierarchical clustering.

Hierarchical clustering algorithm goals at discovering similarity between situations—quantified by a distance metric—to group them into segments referred to as clusters. 

The purpose of the algorithm is to search out clusters such that information factors in a cluster are extra related to one another than they’re to information factors in different clusters.

There are two frequent hierarchical clustering algorithms, every with its personal strategy: 

• Agglomerative Clustering
• Divisive Clustering

Agglomerative Clustering 

Suppose there are n distinct information factors within the dataset. Agglomerative clustering works as follows:

1. Begin with n clusters; every information level is a cluster in itself.
2. Group information factors collectively based mostly on similarity between them. Which means related clusters are merged relying on the gap.
3. Repeat step 2 till there’s just one cluster.

Divisive Clustering

Because the title suggests, divisive clustering tries to carry out the inverse of agglomerative clustering:

1. All of the n information factors are in a single cluster.
2. Divide this single massive cluster into smaller teams. Notice that the grouping collectively of knowledge factors in agglomerative clustering relies on similarity. However splitting them into totally different clusters relies on dissimilarity; information factors in numerous clusters are dissimilar to one another.
3. Repeat till every information level is a cluster in itself.

As talked about, the similarity between information factors is quantified utilizing distance. Generally used distance metrics embody the Euclidean and Manhattan distance.

For any two information factors within the n-dimensional function area, the Euclidean distance between them given by:

One other generally used distance metric is the Manhattan distance given by:

The Minkowski distance is a generalization—for a basic p >= 1—of those distance metrics in an n-dimensional area:

Utilizing the gap metrics, we will compute the gap between any two information factors within the dataset. However you additionally have to outline a distance to find out “how” to group collectively clusters at every step.

Recall that at every step in agglomerative clustering, we choose the two closest teams to merge. That is captured by the linkage criterion. And the generally used linkage standards embody:

• Single linkage
• Full linkage
• Common linkage
• Ward’s linkage

Single Linkage

In single linkage or single-link clustering, the gap between two teams/clusters is taken because the smallest distance between all pairs of knowledge factors within the two clusters.
 

Full Linkage 

In full linkage or complete-link clustering, the gap between two clusters is chosen because the largest distance between all pairs of factors within the two clusters.

Common Linkage

Typically common linkage is used which makes use of the typical of the distances between all pairs of knowledge factors within the two clusters.

Ward’s Linkage

Ward’s linkage goals to decrease the variance throughout the merged clusters: merging clusters ought to decrease the general enhance in variance after merging. This results in extra compact and well-separated clusters.

The gap between two clusters is calculated by contemplating the enhance within the whole sum of squared deviations (variance) from the imply of the merged cluster. The concept is to measure how a lot the variance of the merged cluster will increase in comparison with the variance of the person clusters earlier than merging.

Once we code hierarchical clustering in Python, we’ll use Ward’s linkage, too.

We will visualize the results of clustering as a dendrogram. It’s a hierarchical tree construction that helps us perceive how the info factors—and subsequently clusters—are grouped or merged collectively because the algorithm proceeds.

Within the hierarchical tree construction, the leaves denote the situations or the information factors within the information set. The corresponding distances at which the merging or grouping happens could be inferred from the y-axis.

Pattern Dendrogram | Picture by Writer

As a result of the kind of linkage determines how the info factors are grouped collectively, totally different linkage standards yield totally different dendrograms.

Based mostly on the gap, we will use the dendrogram—reduce or slice it at a selected level—to get the required variety of clusters.

In contrast to some clustering algorithms like Ok-Means clustering, hierarchical clustering doesn’t require you to specify the variety of clusters beforehand. Nevertheless, agglomerative clustering could be computationally very costly when working with massive datasets. 

Subsequent, we’ll carry out hierarchical clustering on the built-in wine dataset—one step at a time. To take action, we’ll leverage the clustering bundle—scipy.cluster—from SciPy.

Step 1 – Import Essential Libraries

First, let’s import the libraries and the required modules from the libraries scikit-learn and SciPy:

# imports
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.datasets import load_wine
from sklearn.preprocessing import MinMaxScaler
from scipy.cluster.hierarchy import dendrogram, linkage

Step 2 – Load and Preprocess the Dataset

Subsequent, we load the wine dataset right into a pandas dataframe. It’s a easy dataset that’s a part of scikit-learn’s datasets and is useful in exploring hierarchical clustering.

# Load the dataset
information = load_wine()
X = information.information

# Convert to DataFrame
wine_df = pd.DataFrame(X, columns=information.feature_names)

Let’s verify the primary few rows of the dataframe:

Truncated output of wine_df.head()

Discover that we’ve loaded solely the options—and never the output label—in order that we will peform clustering to find teams within the dataset. 

Let’s verify the form of the dataframe:

There are 178 data and 14 options:

As a result of the info set incorporates numeric values which are unfold throughout totally different ranges, let’s preprocess the dataset. We’ll use MinMaxScaler to rework every of the options to tackle values within the vary [0, 1].

# Scale the options utilizing MinMaxScaler
scaler = MinMaxScaler()
X_scaled = scaler.fit_transform(X)

Step 3 – Carry out Hierarchical Clustering and Plot the Dendrogram

Let’s compute the linkage matrix, carry out clustering, and plot the dendrogram. We will use linkage from the hierarchy module to calculate the linkage matrix based mostly on Ward’s linkage (set methodology to ‘ward’).

As mentioned, Ward’s linkage minimizes the variance inside every cluster. We then plot the dendrogram to visualise the hierarchical clustering course of.

# Calculate linkage matrix
linked = linkage(X_scaled, methodology='ward')

# Plot dendrogram
plt.determine(figsize=(10, 6),dpi=200)
dendrogram(linked, orientation='high', distance_sort="descending", show_leaf_counts=True)
plt.title('Dendrogram')
plt.xlabel('Samples')
plt.ylabel('Distance')
plt.present()

As a result of we’ve not (but) truncated the dendrogram, we get to visualise how every of the 178 information factors are grouped collectively right into a single cluster. Although that is seemingly troublesome to interpret, we will nonetheless see that there are three totally different clusters.

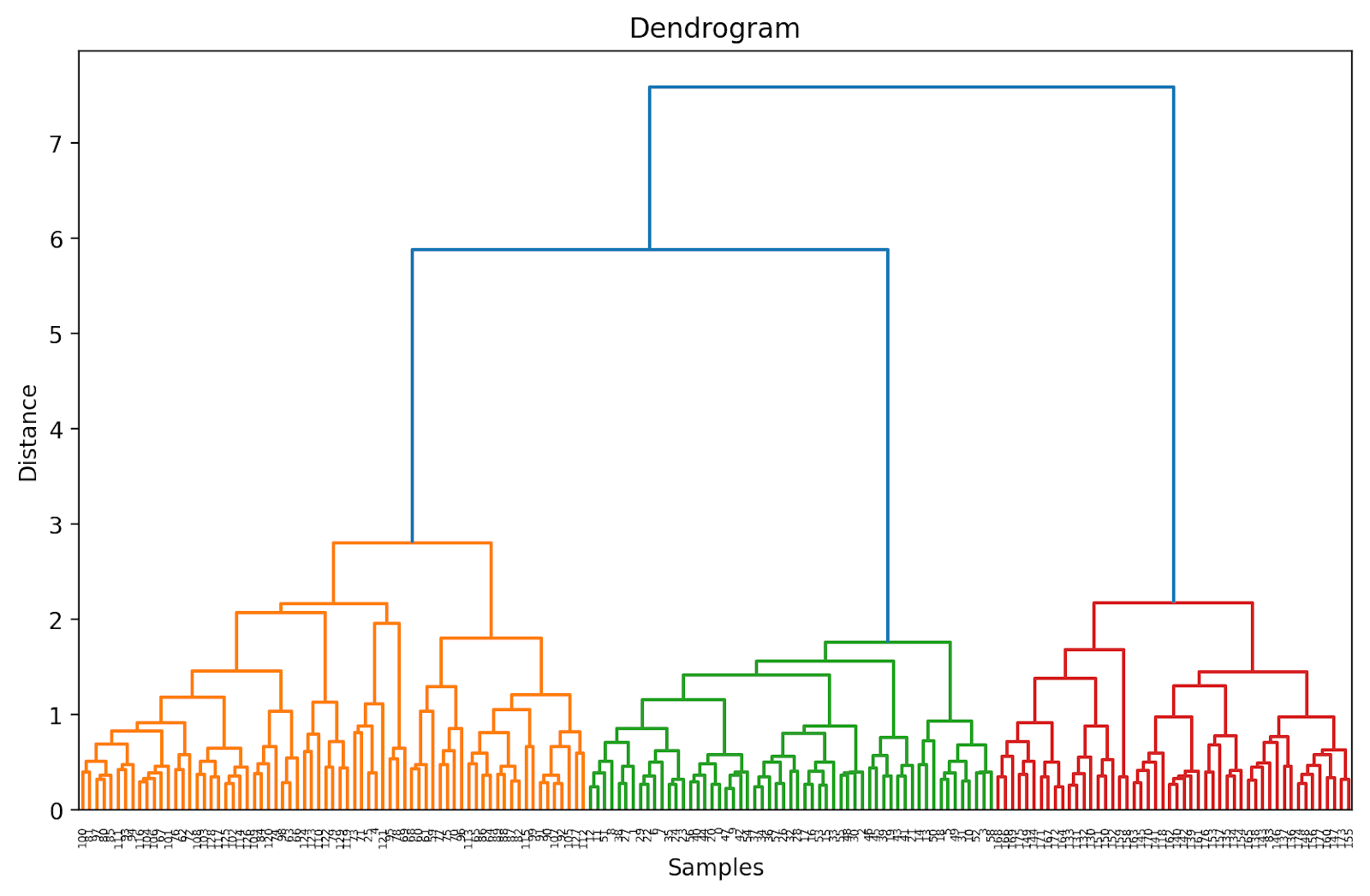
Truncating the Dendrogram for Simpler Visualization

In observe, as a substitute of the complete dendrogram, we will visualize a truncated model that is simpler to interpret and perceive.

To truncate the dendrogram, we will set truncate_mode to ‘degree’ and p = 3. 

# Calculate linkage matrix
linked = linkage(X_scaled, methodology='ward')

# Plot dendrogram
plt.determine(figsize=(10, 6),dpi=200)
dendrogram(linked, orientation='high', distance_sort="descending", truncate_mode="degree", p=3, show_leaf_counts=True)
plt.title('Dendrogram')
plt.xlabel('Samples')
plt.ylabel('Distance')
plt.present()

Doing so will truncate the dendrogram to incorporate solely these clusters that are inside 3 ranges from the ultimate merge.

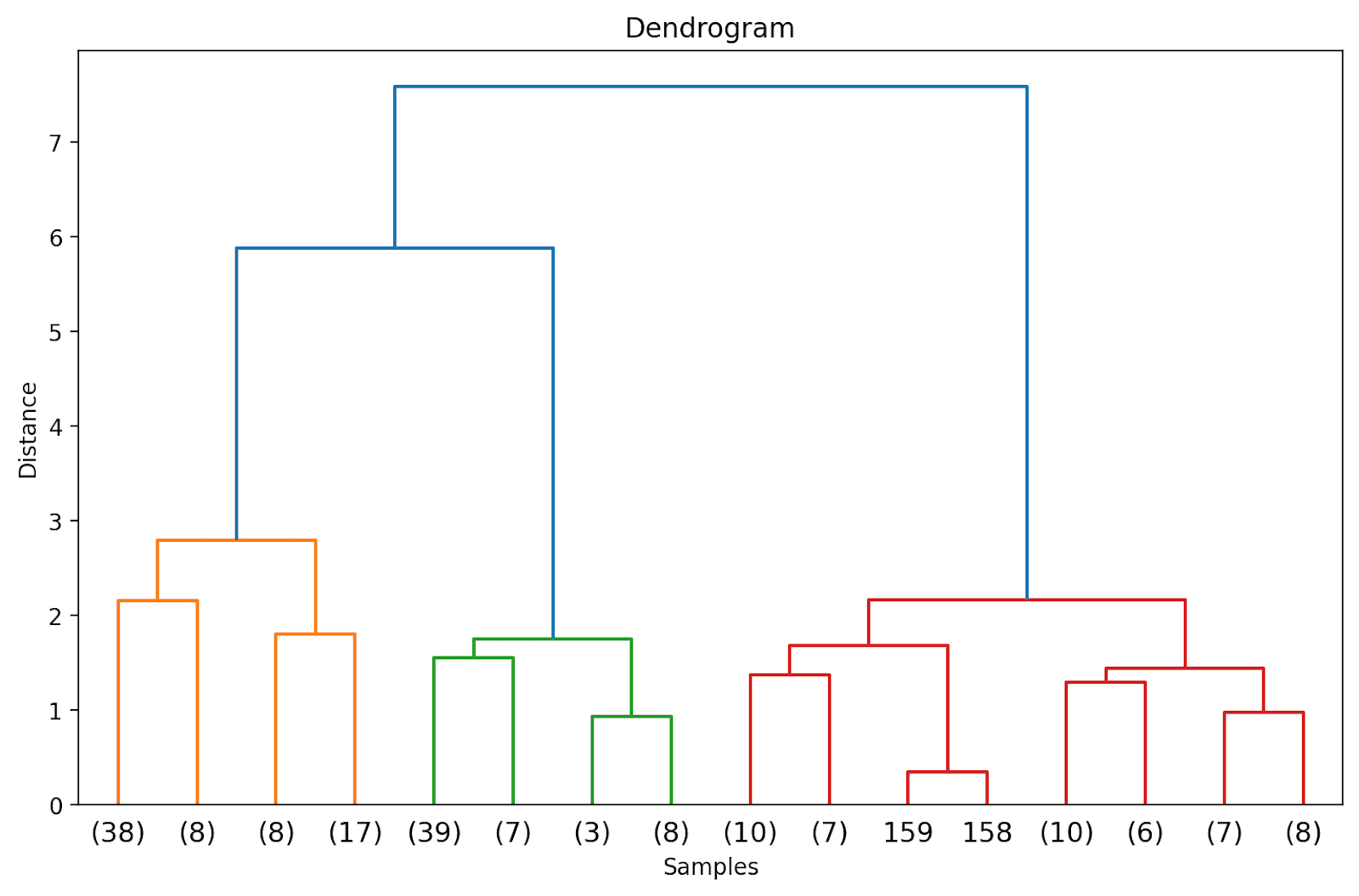
Within the above dendrogram, you may see that some information factors akin to 158 and 159 are represented individually. Whereas some others are talked about inside parentheses; these are not particular person information factors however the variety of information factors in a cluster. (okay) denotes a cluster with okay samples.

Step 4 – Establish the Optimum Variety of Clusters

The dendrogram helps us select the optimum variety of clusters. 

We will observe the place the gap alongside the y-axis will increase drastically, select to truncate the dendrogram at that time—and use the gap as the edge to kind clusters. 

For this instance, the optimum variety of clusters is 3.

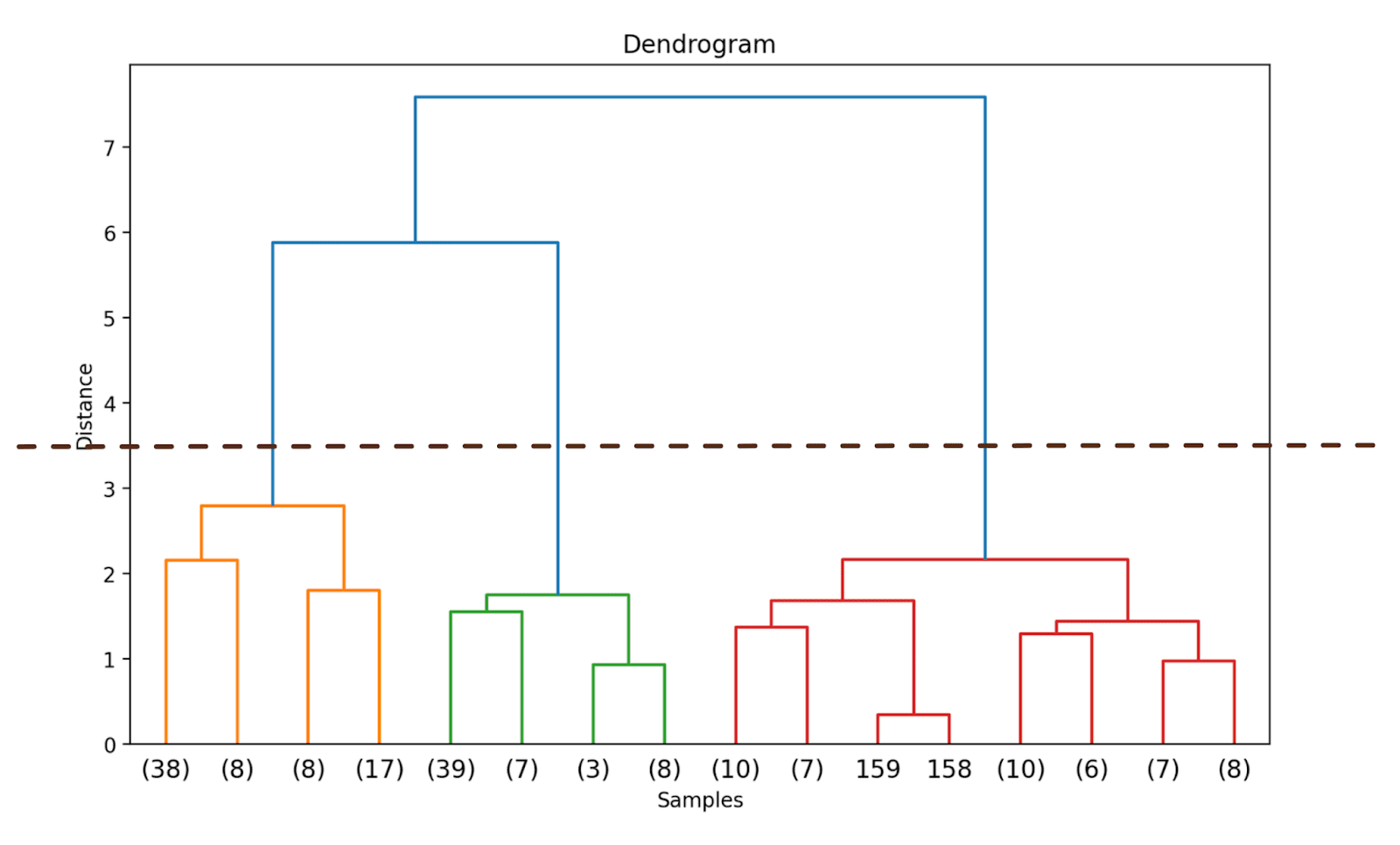
Step 5 – Kind the Clusters 

As soon as now we have selected the optimum variety of clusters, we will use the corresponding distance alongside the y-axis—a threshold distance. This ensures that above the edge distance, the clusters are now not merged. We select a threshold_distance of three.5 (as inferred from the dendrogram).

We then use fcluster with criterion set to ‘distance’ to get the cluster project for all the info factors:

from scipy.cluster.hierarchy import fcluster

# Select a threshold distance based mostly on the dendrogram
threshold_distance = 3.5  

# Reduce the dendrogram to get cluster labels
cluster_labels = fcluster(linked, threshold_distance, criterion='distance')

# Assign cluster labels to the DataFrame
wine_df['cluster'] = cluster_labels

It’s best to now have the ability to see the cluster labels (considered one of {1, 2, 3}) for all the info factors:

print(wine_df['cluster'])

Output >>>
0      2
1      2
2      2
3      2
4      3
      ..
173    1
174    1
175    1
176    1
177    1
Title: cluster, Size: 178, dtype: int32

Step 6 – Visualize the Clusters

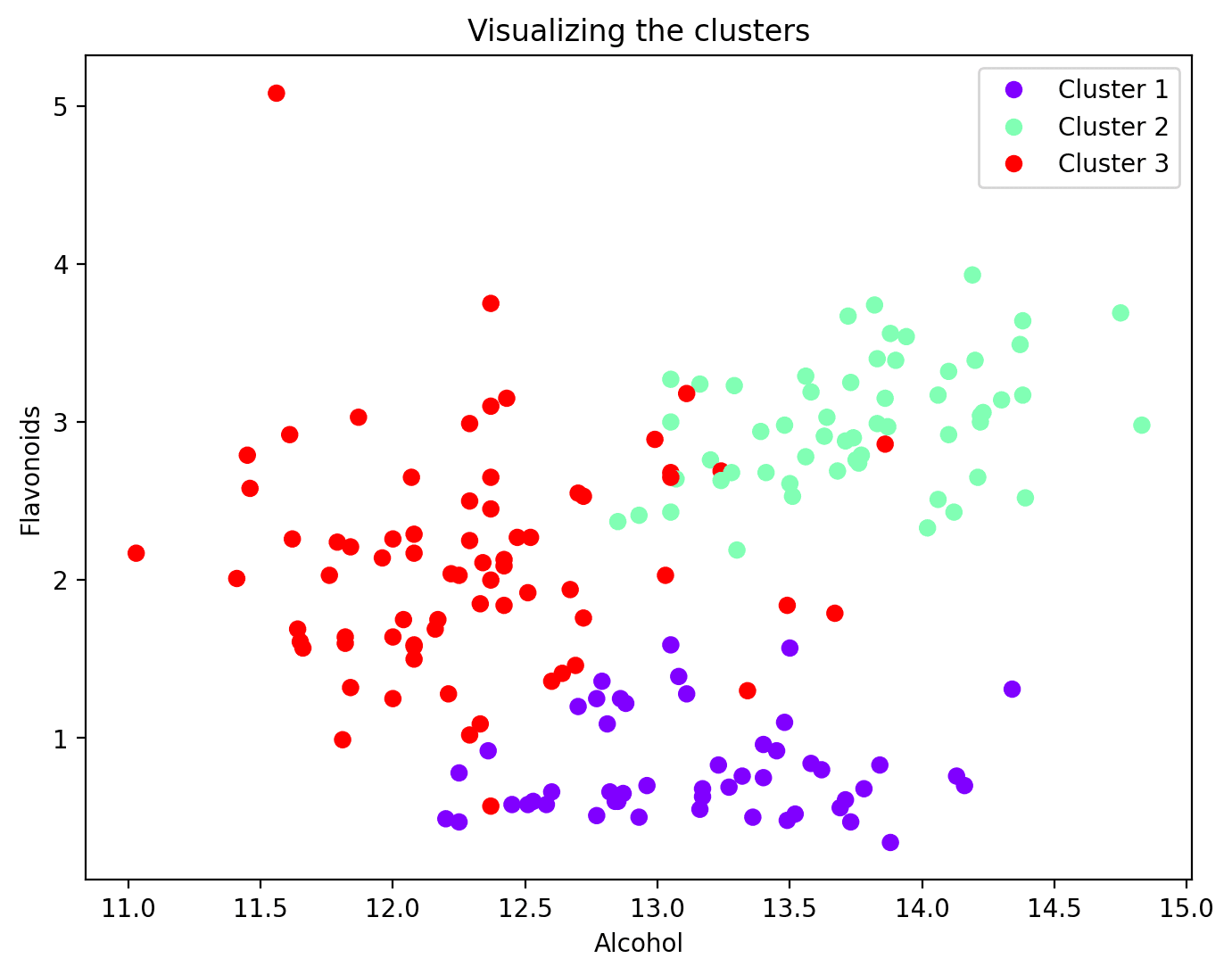
Now that every information level has been assigned to a cluster, you may visualize a subset of options and their cluster assignments. Here is the scatter plot of two such options together with their cluster mapping:

plt.determine(figsize=(8, 6))

scatter = plt.scatter(wine_df['alcohol'], wine_df['flavanoids'], c=wine_df['cluster'], cmap='rainbow')
plt.xlabel('Alcohol')
plt.ylabel('Flavonoids')
plt.title('Visualizing the clusters')

# Add legend
legend_labels = [f'Cluster {i + 1}' for i in range(n_clusters)]
plt.legend(handles=scatter.legend_elements()[0], labels=legend_labels)

plt.present()

And that is a wrap! On this tutorial, we used SciPy to carry out hierarchical clustering simply so we will cowl the steps concerned in better element. Alternatively, you too can use the AgglomerativeClustering class from scikit-learn’s cluster module. Completely satisfied coding clustering!

[1] Introduction to Machine Studying

[2] An Introduction to Statistical Studying (ISLR)
 
 
Bala Priya C is a developer and technical author from India. She likes working on the intersection of math, programming, information science, and content material creation. Her areas of curiosity and experience embody DevOps, information science, and pure language processing. She enjoys studying, writing, coding, and low! At present, she’s engaged on studying and sharing her information with the developer neighborhood by authoring tutorials, how-to guides, opinion items, and extra.